Le Funzioni
In questa parte della tesi andremo a notare la stretta relazione che esiste tra le funzioni in campo matematico e l’applicazione di algoritmi nel campo dell’informatica. Si evince che in molti campi, come quello della crittografia con il metodo RSA, siano presenti funzioni determinate da distinti algoritmi con il quale possono essere calcolate. Inizialmente verrà data una semplice definizione di funzione e i differenti tipi di essa e successivamente del legame tra funzioni e algoritmi.
Funzione: definizione e tipi.
Dati due insiemi A e B, si dice funzione una legge che associa ogni elemento dell’insieme A ad uno e un solo elemento dell’insieme B, dove A e B vengono definiti rispettivamente dominio e codominio della funzione. Una funzione si indica con y = f(x) dove: x è un elemento generico appartenente all’insieme A e viene indicato come f(x). L’insieme A oltre che chiamato dominio spesso viene definito anche come “campo di esistenza”. Si distinguono tre tipi di funzione:
- Funzione iniettiva dove ad elementi distinti dell’insieme A corrispondono elementi distinti dell’insieme B diversamente da quella non iniettiva dove esistono più elementi di A cui corrisponde lo stesso elemento di B.
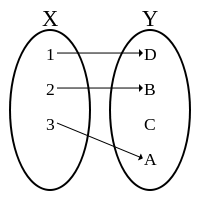
- Funzione suriettiva dove tutti gli elementi di B sono collegati con uno o più elementi di A, invece nella non suriettiva esistono elementi di B non collegati ad elementi dell’insieme A.
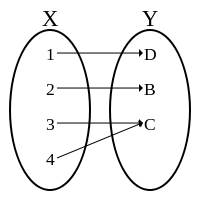
- Funzione biunivoca quando si tratta di corrispondenza sia iniettiva che suriettiva, esempio è quando ogni elemento di A è collegato con un solo elemento di B e l’insieme B viene esaurito.
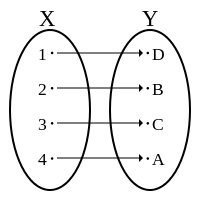
Funzioni e algoritmi.
Come si può capire, l’informatica si occupa del modo di elaborare l’informazione attraverso le macchine. L’elaborazione di informazioni implica anche lo studio dei problemi relativi alla rappresentazione, conservazione e la trasmissione dell’informazione.
Uno dei cardini dell’informatica è la teoria della computabilità che affronta il problema del calcolo delle funzioni mediante procedimenti algoritmici. La teoria della computabilità o della calcolabilità cerca di comprendere quali funzioni possono essere calcolate tramite un procedimento automatico di passi prestabiliti definiti come algoritmo. In altre parole essa cerca di determinare se una data funzione è teoricamente calcolabile, questa disciplina è comune sia alla matematica che all’informatica.
Quindi una determinata funzione si definisce computabile se esiste un algoritmo che la calcola, ovvero in termini matematici, un algoritmo calcola una funzione f(x) se, per ogni possibile valore “in Input” della variabile indipendente xn l’algoritmo fornisce “in Output” f(xn).
Il concetto di algoritmo è correlato, dunque, a quello di agente di calcolo perchè un algoritmo si propone di descrivere azioni espresse in un programma che un esecutore è in grado di eseguire.
Perciò un riassunto comprensivo può essere che: "un linguaggio di programmazione serve a esprimere algoritmi che calcolano funzioni".
Si può dare un concetto di algoritmo più concreto, sotto questo aspetto, con la macchina di Turing(1936 Alan Turing), una macchina ideale che manipola i dati contenuti su un nastro di lunghezza potenzialmente infinita, secondo un insieme prefissato di regole ben definite. In altre parole è un modello astratto che definisce una macchina in grado di eseguire algoritmi.
Prima si è anche parlato di metodo RSA nel campo della crittografia asimmetrica dove il problema è molto semplice: vi sono due persone, il Mittente e il Destinatario che vogliono comunicare fra di loro in modo sicuro. Dato un messaggio "M" il Mittente usa una funzione f(un algoritmo) che trasforma il messaggio "M" in un’altra sequenza "C" che invia, successivamente il Destinatario usa un’altra funzione "g" che trasforma il messaggio "C" nel messaggio originale "M". Per fare ciò si utilizza una chiave pubblica del Destinatario (e) nella fase di criptazione e una chiave privata (d) nella fase di decriptazione.
Le due funzioni f e g di codifica e decodifica hanno come argomento perciò il messaggio e anche la chiave, in simboli si rappresenta:
- Codifica f(M,e) = C;
- Decodifica g(C,d) = M;